ハーツホーン「幾何学I・II」 7節演習問題3

7.7

(a)

線分AB上にA*C*Bとなる点C∈線分ABが存在するとすると、

A, C∈線分AC、B, C∈線分CBは明らか。

A*D*Cとなる点Dが存在すれば、

公理B1によりB*C*AかつC*D*Aだから、

演習問題7.1(b)によりB*D*AとなりD∈線分AB。

同様にC*E*Bとなる点Eが存在すれば、D∈線分AB。

したがって線分ABの点は線分ACまたは線分CBに属するから

線分AC∪線分CB=線分AB。

また、B*C*AからA∉線分CBで、さらにC*D*Aから

練習問題7.1(b)によりB*C*Dだから、D∉線分CB。

同様にB∉線分AC、E∉線分AC。

なので、線分AC∩線分AC={C}。

(b)

ℓ上の任意の点Pは、Aに関してBと同じ側にあるか、

反対側にあるか、A自身であるかのいずれかである。

PがBと同じ側にあるかA自身なら、P∈半直線AB。

PがBと反対側にあれば、B*A*Pだから PはBに関してAと同じ側にある。

したがってP∈半直線BA。よって半直線AB∪半直線BA=ℓ。

また、PがAまたはBと一致すればP∈半直線AB∩半直線BAである事は明らか。

A*P*BならPはBに関してAと同じ側にあり、

かつAに関してBと同じ側にあるから、P∈半直線AB∩半直線BA。

したがって線分AB⊆半直線AB∩半直線BA。

逆にPはBに関してAと同じ側にあり、

かつAに関してBと同じ側にあるなら、A*P*Bだから、

線分AB⊇半直線AB∩半直線BA。

したがって、線分AB=半直線AB∩半直線BA。

7.8

演習問題7.6の（下手な方の）証明で示した。

7.9

次の補題をまず証明する。

補題：線分AB上にA*C*Bとなる点Cが存在するとする。

線分ABと共線的でない点Dをとると、Cは∠ADBの内部にある。

∵) A*C*BよりCは直線ADについてBと同じ側にあり、

かつ直線BDについてAと同じ側にあるから、Cは∠ADBの内部にある。

この補題を用いて証明する。

演習問題7.6により辺BC上にB,Cと異なる点Dが存在するので、

線分ADが存在する。また、辺AC上にA,Cと異なる点Eが存在するので、

線分BEが存在する。

△ACDにおいて直線BEはPaschの公理B4の条件を満たすから、

直線BEは線分ADまたは線分DCと交わるが、

直線BEと直線DCとの交点はBだから、直線BEは線分ADと交わる。

したがって直線BEと線分ADとの交点Fが存在する。

Fは線分AD上にあるから、補題により∠ACDすなわち∠ACBと、

∠ABCの内部の点である。またFは線分BE上にあるから、

補題により∠BAEすなわち∠BACの内部の点である。

したがってFは△ABCの内部の点だから、三角形の内部は空集合でない。

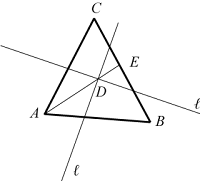
7.10

半直線ADが存在するので、命題7.3（横木定理）により、

半直線ADと辺BCとの交点Eが存在する。

ℓがAを通ればℓ は直線ADと一致するから、辺BCと交点Eで交わる。

同様にℓがBまたはCを通れば、辺ACまたは辺ABとそれぞれ交わる。

ℓがA,B,Cのいずれも通らなければ、Dが直線ADとℓの交点だから、

ℓは直線AD上の点Eを通らない。ゆえに△ACEにおいて、

ℓはPaschの公理B4の条件を満たすから、辺ACまたは辺ECと交わる。

演習問題7.7(a)により辺EC⊆辺ACだから、

ℓは辺ACまたは辺BCと交わる。