二等辺三角形の流儀

「二等辺三角形の2つの底角は互いに等しい。」

中学校でやる二等辺三角形の「底角定理」だが、意外に議論の余地があったりする。
中学数学でも、ユークリッドでも、ヒルベルトでも、ハーツホーンでも、
まだ公理や定理があまり出てきていないうちに証明されるため、
何を公理にとったか、その公理をどう使うことを許すか、によって証明が変わってくるからだ。


1. 中学数学流

中学数学では三角形の合同三条件を公理として要請している。

なので、よくある定番の証明は

（証明）

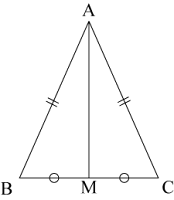
AB=ACの二等辺三角形ABCにおいて、

BCの中点Mを取り、AMを結ぶ。

△AMBと△AMCにおいて、

仮定によりAB=AC、

MはBCの中点なのでBM=CM、

共通なのでAM=AM。

故に三辺相等により△AMB≡△AMC。

対応する角は等しいので∠B=∠C。

教育的に分かりやすい証明。

ついでにAMがBCの垂直二等分線で∠Aの二等分線でもあることがわかるので、
何かと便利。

2. ユークリッド流

ユークリッド

原論

ユークリッド「原論」では定理1-5。いわゆる「ロバの橋の証明」
（＝幾何学に不慣れな者が挫折する、「原論」最初の難所）。

まだ三辺相等の合同条件は出てきていない（定理1-8）。

細かいことを言えば正確には、三辺相等はユークリッドでは、
三角形の合同条件ではない。

定理1-8は三辺相等なら対応する角が等しいと述べているだけである。

まあ三角形の合同の使い道はさしあたりそれくらいしかないので、
どっちでもいいことだが。

定理1-8の三辺相等の証明に底角定理を使っているので、

上の中学数学の証明だと循環論法になってしまう。
また、中学数学的には頂角の二等分線を使う手もあるのだが、
「原論」では、頂角の二等分線の存在は、
定理1-9で三辺相等を使って証明されるので、
ここで頂角の二等分線を使ってしまったらやはり循環論法。

なので中学とは別の証明が必要になる。主な使える材料は

• 二辺夾角相等の合同定理（定理1-4）
• 2つの角または2つの線分の間には大小・等しい関係があり、和や差が定義できる（暗黙の前提）
• a=b, c=dならa-c=b-d（公理1-3）

である。

（証明）

AB=ACの二等辺三角形ABCにおいて、ABを延長した延長線上に点Fをとり、

AFの延長上に点Dをとる。ACの延長上に、AF=AGとなる点Gをとり、

AGの延長上に点Eをとる。

△AFCと△AGBにおいて、

仮定によりAF=AG (1)

仮定によりAC=AB (2)

共通な角なので∠A=∠A

これらにより二辺夾角相等（定理1-4）から、⊿AFC≡⊿AGB

対応する角は等しいので∠ACF=∠ABG  (3)

対応する角は等しいので∠AFC=∠AGB  (4)

対応する辺は等しいのでFC=GB (5)

また、△FBCと△GCBにおいて、

(1)から(2)を引いて、公理1-3により　BF=CG

これと(4)(5)から二辺夾角相等（定理1-4）により△FBC≡△GCB

対応する角は等しいので、∠FCB=∠GBC (6)

(3)から(6)を引いて、公理1-3により　∠ABC=∠ACB

3. ヒルベルト流

ヒルベルト

幾何学基礎論

ヒルベルト「幾何学基礎論」では底角定理は定理11。
ヒルベルトは幾何学の厳密化のため、必要最低限の公理しか要請しないで、
その公理の範囲内でどこまでの定理が成り立つか示すことに
力点を置いているので、
底角定理の証明の段階では使える材料は非常に少ない。

• 線分や、角の合同関係（公理III4）はあるが、大小関係はまだ定義されていない。
• 二辺夾角相等なら他の対応する角も互いに等しい（公理III5）（三角形の合同自体は要請しない、というかまだ定義されていない。）。

しかしヒルベルトではユークリッドの時代と違い、

「合同は異なる位置にある2つの図形を比べるもの」というだけではなく、
「図形が一つあれば自分自身と比べられる」という発想があることがポイント。

ヒルベルトは「証明される」と言っているだけだが、こういう証明だろう。

（証明）

△ABCにおいてAB=ACである。

△ABCと△ACBにおいて、

仮定によりAB=AC

仮定によりAC=AB

共通なので∠BAC=∠CAB

したがって公理III5により∠ABC=∠ACB

ヒルベルト流は、まあ間違いなく教育的ではないｗ
背理法が出てこない分、まだ中学生に理解できなくもないだろうが、
ちょっと混乱を招くだろうなあ。

ヘレニズムの昔から、「自分自身と比べる」発想はあっただろうし、
ヒルベルト流の証明はユークリッドも知っていたんじゃないかと思う（別に根拠はない）し、
実際、4世紀にはパップス（パッポス）がこの方法での証明を書き残しているらしい。
でもユークリッドが「原論」に取り入れなかったのは、
「邪道」というか受け入れがたいからなのだろうか。
ヒルベルト流の「自分自身との比較」は、
「原論」の他の部分や中学数学での図形の扱い方からは外れているから、
中学数学の証明に慣れた目には、ぱっと見て違和感を覚えるのは確かだな。

対称性や変換の概念が発達して、自分自身を変換する記述が普通になってきた
19世紀になってはじめて、ヒルベルト流も普通に受け入れられるようになったのかな。

ハーツホーン

幾何学II

ハーツホーン

幾何学I

4. ハーツホーン流

ハーツホーン「幾何学I」では、公理系はヒルベルトのものに近いが、

• 線分や角の合同と大小関係・和や差を定義
• 二辺夾角相等の合同公理（公理C6）を要請

などを行ってから底角定理の証明に入る。
証明はユークリッド流と基本的に同じである。

ヒルベルト流でも無論問題ないのだが、ハーツホーンではユークリッド「原論」の論理を、
現代的観点からチェックすることにポイントが置かれているので、
あえてユークリッド流でやっている。

と、いろいろ事情が複雑な底角定理の証明。

「で、結局どの流儀でやるのが正しいの」という議論を見かけるが、

「何を公理として要請したかによる」というのが答え。

まあ、上記のどの公理系でも使えて一番あざやかなのはヒルベルト流だと思うが、

中学生相手、という教育的観点が入ってくるとやっぱ現実的じゃないなあ。

ちなみに、逆定理「二つの角が等しい三角形は二等辺三角形である」は、
ユークリッドは底角定理のすぐあと（定理1-6）、
ヒルベルトは角の大小関係について長々と準備したあと（定理24）で、
両方とも背理法で証明している。ここまで平行線公理は使っていない。

が、背理法を論理として認めない（ていうかまだやってない）中学数学では、
AからBCに垂線をおろして三角形の内角の和が二直角であることを使った証明、
つまり平行線公理を要請した証明が定番。
平行線公理を使わずに証明できるんだろうか？